Overflødig det som er. Betydningen av konseptet

2024 Forfatter: Henry Conors | [email protected]. Sist endret: 2024-02-12 11:36

Artikkelen beskriver statistikkens rolle som vitenskap. Konseptet kurtosis og dets bruk i vitenskapen vurderes.

Statistics. Grunnleggende konsept

Statistikk er det grunnleggende derivatet av matematisk vitenskap. Dette faget tilhører en rekke sosiale disipliner som har som mål å danne et bilde av verdensbildet og en kompetent analyse av hendelser hos elever.

Statistikk studerer alle slags prosesser og hendelser i menneskers liv, fremhever deres mønstre og presenterer alt i form av korte statistiske rapporter. Slik vitenskap er samfunnsnyttig og krever stadige forbedringer. Overskudd - hva er det? Dette er et grunnleggende konsept i grafisk statistikk som hjelper til med å bestemme riktigheten av perfekt kalkulus. Kurtosis bør ikke ha et sterkt avvik.

Statistics lar deg tilfredsstille folks behov for pålitelig informasjon om et bestemt fenomen, hendelse og så videre. Å bestemme dynamikken til livsfaktorer, deres tilbakegang, stagnasjon eller vekst - dette er nøyaktig hva denne vitenskapen gjør.

I den moderne verden opptar statistikk en av hovedplassene på den vitenskapelige arenaen. La oss vurdere konseptet "kurtosis". Hva er et statistisk mål og observasjon? Hvor brukes disse konseptene? Les mer om alt dette iartikkel.

Hva er kurtosis i statistikk?

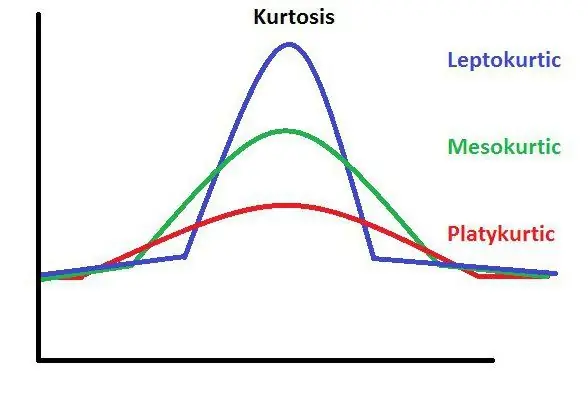
Kurtosis er et statistisk konsept som representerer skarpheten til hver topp i en distribusjonsgraf. Det er en spesiell formel for den nøyaktige beregningen.

Forventning sier at for en jevnere fordeling av statistiske data, må kurtosis være lik et positivt tall. Bokstavelig t alt betyr dette konseptet et visst avvik fra normen og ytterligere unormal utvikling eller funksjon av det statistiske systemet.

Overdreven uttrykk for kurtose på en statistisk graf kan indikere en feil studie eller feil i de originale dataene til grafen. Et slikt konsept er skalært av natur, noe som betyr at den endelige beregningen skal resultere i et tall som ikke vil inneholde variabler eller hjelpefunksjoner. Slik ser kurtosis ut.

Hva er symmetrisk og asymmetrisk distribusjon

Kurtosis, som er relatert til fordelingen av den symmetriske typen, er lik null. Dette kan tydelig vises med en graf. Den asymmetriske grafen viser et tall som ikke er null. Dette er hvordan kurtosis betegnes.

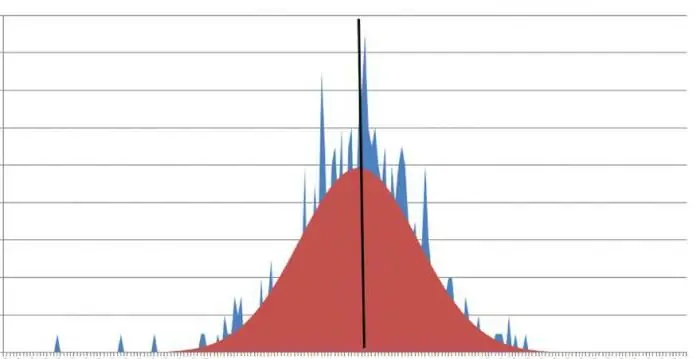
Hva er skarpheten til en topp? En graf som har skarpe topper indikerer at kurtosisverdien er et tall mindre enn null. Ofte er det situasjoner der et gitt konsept ikke kan uttrykkes med en egen verdi. I dette tilfellet nærmer det seg minus eller pluss uendelig.